Amino Acid Substitutions & Replacement Matrices
Mutation prabability matrix
The previous page discussed the need for a scoring scheme to score amino acid replacements for an accurate sequence alignment. A scoring scheme only based on identities is not very effective. It will miss much helpful information, especially when we need to detect weak homology. When discussing amino acid replacement schemes, we must remember that during evolution, amino acids may be replaced by the original type after several cycles. Such a process is logical since the conservation of structure and function always has higher priority in the selection process. This type of conservation has also been described as conservation of size and hydrophobicity (Taylor, 1986).
Margaret Dayhoff and co-workers, who pioneered the field of protein sequence analysis, databases, and bioinformatics, developed the first mutation probability matrix in the 1970s. Their model was based on observed frequencies of substitutions of each of the 20 amino acids derived from an alignment of closely related sequences. Based on the number of common amino acids (20), we can count 210 possible replacement pairs, of which 190 pairs correspond to two different amino acids and 20 pairs of identical substitutions. In the resulting so-called mutation probability matrix, each element Mij provides an estimate of the probability of an amino acid in column j to be mutated to the amino acid in row i after a particular evolutionary time.
Margaret Dayhoff and co-workers, who pioneered the field of protein sequence analysis, databases, and bioinformatics, developed the first mutation probability matrix in the 1970s. Their model was based on observed frequencies of substitutions of each of the 20 amino acids derived from an alignment of closely related sequences. Based on the number of common amino acids (20), we can count 210 possible replacement pairs, of which 190 pairs correspond to two different amino acids and 20 pairs of identical substitutions. In the resulting so-called mutation probability matrix, each element Mij provides an estimate of the probability of an amino acid in column j to be mutated to the amino acid in row i after a particular evolutionary time.
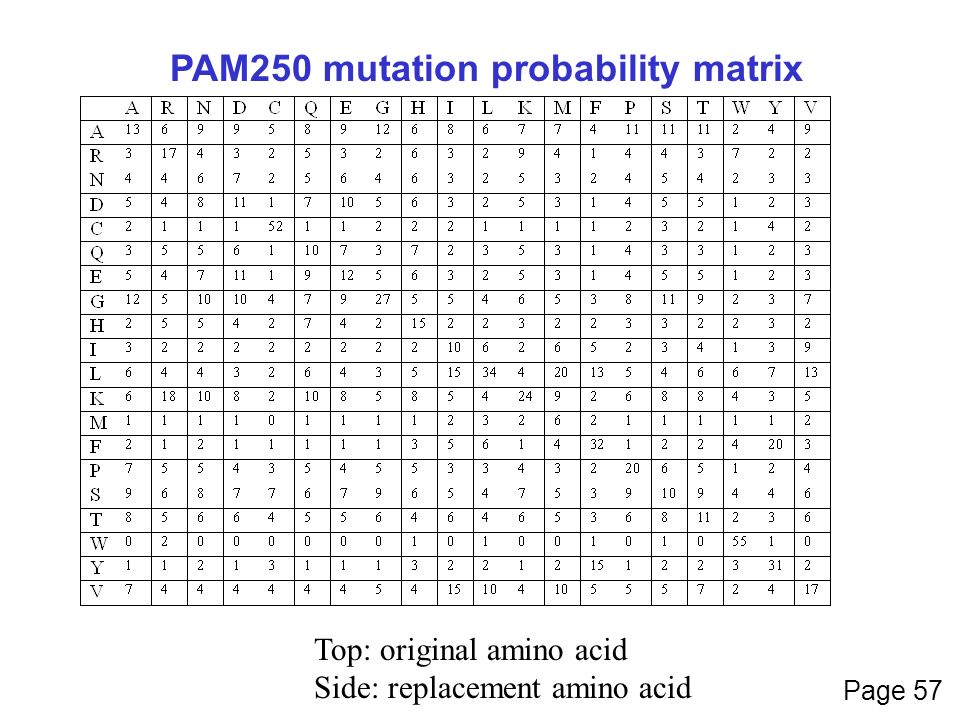
Image from Byron Holland: https://slideplayer.com/slide/8888934/
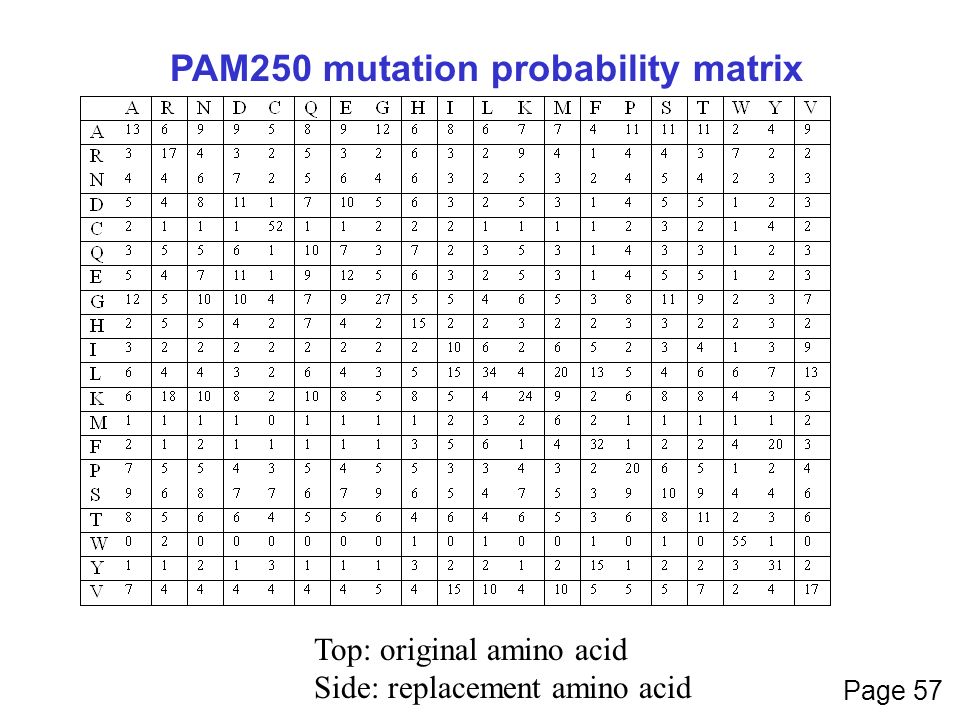
Image from Byron Holland: https://slideplayer.com/slide/8888934/
An evolutionary unit of 100 million years was adapted, resulting in the PAM (Percentage Accepted Mutations / 100 million years) matrix. 1 PAM corresponds to an average amino acid substitution in 1% of all positions. Although 100 PAM does not mean that all the amino acids in the sequence are different (as compared to the original sequence), since, as noted above, many of them will be mutated back to their original type.
Further analysis showed that, although at 256 PAM, 80 % of all amino acids will be substituted, 48% of Trp, 41% of Cys, and 20% of His will be conserved. On the other hand, only 7% of S residues will remain (discussed in Barton, J, 1996). This conservation pattern presumably results from a combination of structural and functional restraints mentioned above. For example, tryptophan has a large side chain, and if positioned within the structure's core, its replacement by another amino acid may destabilize the protein. In addition, the other highly conserved residues, cysteine and histidine, are often involved in specific functions like proton abstraction (His), metal binding (His and Cys), or disulfide bridge formation (Cys).
After the construction of the mutation probability matrix, Dayhoff et al. defined the score Si,j of two aligned residues i, j according to the following equation:
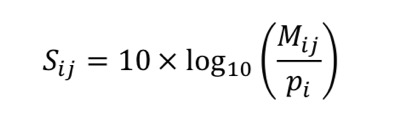
In which (Mij ) is the probability of these two residues being aligned (from the matrix above), and pi - the probability of these two amino acids being aligned by chance.
This type of scoring will give higher numbers to the alignment of a pair of similar amino acids (e.g., Leu and Ile) and lower numbers when the amino acids are different (like I and D). Using this definition, the probability matrix (shown in the image above) can then be used to derive the so-called log-odds scoring matrix:
Further analysis showed that, although at 256 PAM, 80 % of all amino acids will be substituted, 48% of Trp, 41% of Cys, and 20% of His will be conserved. On the other hand, only 7% of S residues will remain (discussed in Barton, J, 1996). This conservation pattern presumably results from a combination of structural and functional restraints mentioned above. For example, tryptophan has a large side chain, and if positioned within the structure's core, its replacement by another amino acid may destabilize the protein. In addition, the other highly conserved residues, cysteine and histidine, are often involved in specific functions like proton abstraction (His), metal binding (His and Cys), or disulfide bridge formation (Cys).
After the construction of the mutation probability matrix, Dayhoff et al. defined the score Si,j of two aligned residues i, j according to the following equation:
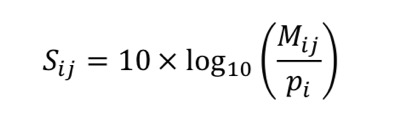
In which (Mij ) is the probability of these two residues being aligned (from the matrix above), and pi - the probability of these two amino acids being aligned by chance.
This type of scoring will give higher numbers to the alignment of a pair of similar amino acids (e.g., Leu and Ile) and lower numbers when the amino acids are different (like I and D). Using this definition, the probability matrix (shown in the image above) can then be used to derive the so-called log-odds scoring matrix:
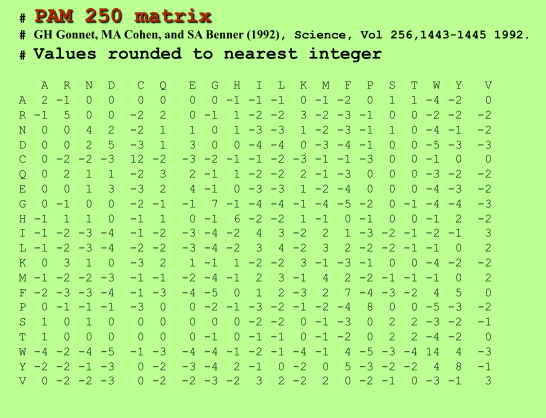
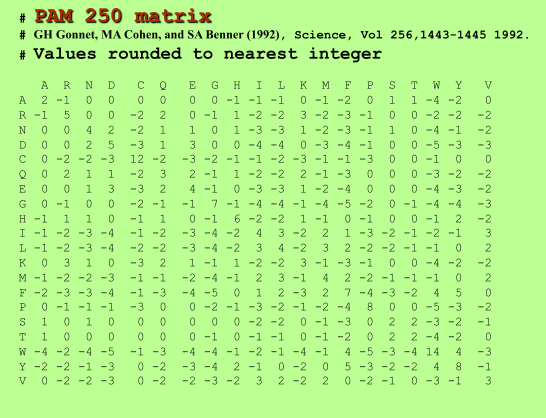
This replacement matrix can be used for the calculation of the alignment score according to the equation discussed earlier: (score) S= Σ of costs (identities, replacements) - Σ of penalties (number of gaps x gap penalties)
Матрицы PAM, PET91 & BLOSUM
В последствии были созданы различные версии матрицы замен, которые служат разным целям. Например, матрицы с низкими значениями PAM (20, 40, 60) предпочтительны при сканировании базы данных, когда выводятся выравнивания коротких, эволюционно близких последовательностей. Чем выше число PAM, тем больше ожидаемое эволюционное расстояние между белками. Это делает матрицы с высоким содержанием PAM подходящими для выравнивания более отдаленных белков, и они будут находить более отдаленные гомологи, если их использовать для сканирования базы данных. Многие интернет-ресурсы по выравниванию последовательностей предоставляют возможность выбора матрицы замещения для выравнивания.
Первоначальная матрица Дейхоффа была основана на ограниченном наборе известных белковых последовательностей, и для многих из 190 возможных замен не удалось собрать достаточно статистических данных. Это было исправлено позже, когда стало доступно больше данных. Примером может служить PET91, обновленная матрица Dayhoff (Jones et al., 1992), основанная на 2621 семействе белков из базы данных SwissProt (теперь UniProt, часть сервера Expasy). Между тем, другие матрицы замещения были разработаны на несколько иных принципах. Одной из самых популярных является матрица BLOSUM (BLOcks of Amino Acid SUbstitution Matrix, Henikoff S, Henikoff JG. 1992). BLOSUM оценивает аминокислотные замены на основе частоты аминокислотных замен в выровненных блоках последовательностей без пробелов (gaps) с определенным процентом оценки идентичности. Таким образом, существует значительная разница между матрицами PAM и BLOSUM - матрицы PAM основаны на мутациях, наблюдаемых при глобальном выравнивании, которое включает высококонсервативные области и низкоконсервативные области с выравниванием с пробелами. Числа, связанные с каждой матрицей (например, BLOSUM62, BLOSUM80 и т. д.), относятся к проценту идентичности последовательностей, выровненных внутри блока. Чем выше номер матрицы тем выше идентичность последовательностей и тем короче эволюционное расстояниям между белками которые использовались для вывода матрицы. BLOSUM с большими номерами используется для последовательностей, о которых известно, что они гомологичны с хорошим уровнем идентичности последовательностей. В то же время для отдаленно родственных белков следует использовать низкие числа BLOSUM.
Первоначальная матрица Дейхоффа была основана на ограниченном наборе известных белковых последовательностей, и для многих из 190 возможных замен не удалось собрать достаточно статистических данных. Это было исправлено позже, когда стало доступно больше данных. Примером может служить PET91, обновленная матрица Dayhoff (Jones et al., 1992), основанная на 2621 семействе белков из базы данных SwissProt (теперь UniProt, часть сервера Expasy). Между тем, другие матрицы замещения были разработаны на несколько иных принципах. Одной из самых популярных является матрица BLOSUM (BLOcks of Amino Acid SUbstitution Matrix, Henikoff S, Henikoff JG. 1992). BLOSUM оценивает аминокислотные замены на основе частоты аминокислотных замен в выровненных блоках последовательностей без пробелов (gaps) с определенным процентом оценки идентичности. Таким образом, существует значительная разница между матрицами PAM и BLOSUM - матрицы PAM основаны на мутациях, наблюдаемых при глобальном выравнивании, которое включает высококонсервативные области и низкоконсервативные области с выравниванием с пробелами. Числа, связанные с каждой матрицей (например, BLOSUM62, BLOSUM80 и т. д.), относятся к проценту идентичности последовательностей, выровненных внутри блока. Чем выше номер матрицы тем выше идентичность последовательностей и тем короче эволюционное расстояниям между белками которые использовались для вывода матрицы. BLOSUM с большими номерами используется для последовательностей, о которых известно, что они гомологичны с хорошим уровнем идентичности последовательностей. В то же время для отдаленно родственных белков следует использовать низкие числа BLOSUM.
Выравнивание на основе структуры
Трехмерная структура белка содержит важную информацию о положении и длине элементов вторичной структуры и расположении петель. Поскольку многие пробелы в выравнивании последовательности возникают в областях между элементами вторичной структуры (менее консервативные участки), использование информации из трехмерной структуры обеспечит более точное позиционирование вставок и делеций в выравнивании. Многие графические программы включают суперпозицию трехмерных структур и обеспечивают выравнивание последовательностей на основе суперпозиции. Однако это выравнивание все еще необходимо проверить, например, путем анализа трехмерной структуры и сравнения сгенерированного структурного выравнивания с множественным выравниванием нескольких последовательностей.
Заключительные замечания
В этом кратком обзоре обсуждаются некоторые основные концепции выравнивания последовательностей. Поскольку, как упоминалось ранее, здесь мы сосредоточены на практическом применении выравнивания и анализа последовательностей, я не стал вдаваться в подробности статистического анализа, стоящего за построением матриц замещения, или данных, связанных с цонсервацией последовательностей.
Заключительные замечания
В этом кратком обзоре обсуждаются некоторые основные концепции выравнивания последовательностей. Поскольку, как упоминалось ранее, здесь мы сосредоточены на практическом применении выравнивания и анализа последовательностей, я не стал вдаваться в подробности статистического анализа, стоящего за построением матриц замещения, или данных, связанных с цонсервацией последовательностей.